একটা বলকে উপরে ছুঁড়ে মারলেন । বলটা একসময় মাটিতে এসে পড়বে । একটা খেলনা গাড়িকে সামনে চলতে লাগিয়ে দিলেন । গাড়ির ব্যাটারীর শক্তি শেষ না হওয়া পর্যন্ত গাড়িটা চলতেই থাকবে । একটা বস্তুকে সুতোর এক প্রান্তে বেঁধে অপর প্রান্ত ধরে চারদিকে ঘুরাতে লাগলেন । সেটা আপনার চারদিকে একটা নির্দিষ্ট বেগে ঘুরবে । এসবই পদার্থবিজ্ঞান অনুযায়ী কিছু গতীয় ব্যাপার । বলকে ছুঁড়ে মারার বিষয়টা দ্বিমাত্রিক এবং রৈখিক গতি । গাড়ির সামনে চলতে থাকা একমাত্রিক এবং রৈখিক গতি । আর বস্তুকে সুতোর প্রান্তে বেঁধে চারদিকে ঘুরানো বৃত্তাকার গতি (Circular Motion) । কিন্তু আমাদের চারপার্শ্বে এসব গতির বাইরেও আরেকটা খুব কমন গতির সাথে আমরা কমবেশী সবাই পরিচিত । তা হল- পর্যাবৃত্ত গতি । আর এই পর্যাবৃত্ত গতির মাধ্যমেই প্রকাশ করা যায় তরঙ্গ, শব্দ, আলো, নদীর স্রোত, পেন্ডুলাম, বেতার তরঙ্গ, মাইক্রোওয়েভ এবং আপনি যে এই টিউটোরিয়াল পড়ছেন ইন্টারনেটের মাধ্যমে সেই ইন্টারনেটের ক্ষেত্রে ব্যবহৃত তড়িৎচৌম্বক তরঙ্গ প্রভৃতি বাস্তব জীবনের অনেক গুরুত্বপূর্ণ সব বিষয় । তাই আমার পরবর্তী এক্সপেরিমেন্ট হিসেবে পর্যাবৃত্ত গতি এবং তরঙ্গকেই বেছে নিতে হল । তো চলুন আজকে শুরু করা যাক আলোচনার বিষয়গুলো দিয়েঃ-

যদিও ইচ্ছে ছিলো আজকে পর্যাবৃত্ত গতি আর তরঙ্গ নিয়ে একটু বিস্তারিত আলোচনা করব । তবে একাডেমিক প্রেসারের কারনে খুব বেশী দূর অগ্রসর হওয়া সম্ভব হলোনা । তাই আজকের আলোচনা নিচের বিষয়গুলোর মধ্যেই সীমাবদ্ধ রাখবঃ-

১। পর্যাবৃত্ত গতি এবং সরল ছন্দিত স্পন্দন । বাস্তবতা এবং আমাদের ধারণা । (ভার্চুয়াল রিয়েলিটি)

২। অভিকর্ষজ তরঙ্গ ও তরঙ্গের বাস্তব রুপ অংকন (এক্সপেরিমেন্ট সহ)

৩। সরল দোলক (ভার্চুয়াল পেন্ডুলাম তৈরীর পদ্ধতি)

এক্সপেরিমেন্টগুলো যেন সহজে বোধগম্য হয় তার জন্য সবগুলোর সাথে লাইভ ডেমো লিংক এবং সোর্স কোড দিয়ে দিয়েছি ।

পদার্থবিজ্ঞান শব্দটা শুনতেই যদি আপনার কাছে গ্রন্থগত কিছু বিষয় আর একগাদা সমীকরণ চোখের সামনে ভেসে ওঠে তাহলে পদার্থবিজ্ঞান নিয়ে আপনার ধারণা সম্পূর্ণ নয় । প্রথমত, পদার্থবিজ্ঞান কেবলমাত্র কোনো গ্রন্থগত বিষয় নয় । আমাদের চারপার্শ্বে আমাদের দৃষ্টিসীমার ভেতরে বা বাইরে যা কিছু ঘটে তা কিভাবে ঘটে এবং কেন ঘটে এসব নিয়ে বিশ্লেষণধর্মী বিজ্ঞানই হল পদার্থবিজ্ঞান । আর গাণিতিক সমীকরণগুলো আমাদের চারপার্শ্বের বস্তুসমূহের ক্রিয়ার বিভিন্ন পরিমাণ নির্ণয়ের মাধ্যম ।

আমাদের চারপার্শ্বের যে জগত, যেখানে আমরা বাস করছি, সেখানে প্রত্যেক বস্তুরই কিছু সাধারণ আচরণ থাকে, বৈশিষ্ট্য থাকে । এসব নিয়ে আলোচনাই পদার্থবিজ্ঞান । আমাদের চারপার্শ্বে কি ঘটছে এবং কেন ঘটছে তার ব্যাখ্যাই পদার্থবিজ্ঞান ।

পদার্থবিজ্ঞান একদিকে যেমন আমাদের শেখাচ্ছে বস্তু কিভাবে কাজ করে এবং পৃথিবী কিভাবে কাজ করে, তেমনি আমাদের দেখাচ্ছে কি কি বৈশিষ্ট্য দিয়ে একটা সম্পূর্ণ জগত সৃষ্টি করা সম্ভব ।

আমাদের চারপার্শ্বে যেসব বিষয় বাস্তবে ঘটে সেগুলোকে অবাস্তব কোনো মাধ্যমে (যেমনঃ কম্পিউটার) ফুটিয়ে তোলাই ভার্চুয়াল রিয়েলিটি । একটা ফুটবল ছুড়ে মারলে সামনে এগিয়ে যায় । এটা বাস্তব । যদি কম্পিউটারেও একটা ফুটবল এঁকে তাকে বাস্তব ফুটবলের মত বৈশিষ্ট্য (যেমন ছুড়লে সামনে এগিয়ে যাওয়া) দেওয়া যায় তাহলে সেই আঁকানো ফুটবলটাই ভার্চুয়াল রিয়েলিটি । আপনার স্কাইপ ভিডিও কলকেও এক প্রকার ভার্চুয়াল রিয়েলিটি বলা যায় । অর্থাৎ, বাস্তব জিনিসকে অবাস্তব মাধ্যমে বাস্তবের মত করে ফুটিয়ে তোলাই ভার্চুয়াল রিয়েলিটির মূল উদ্দেশ্য ।

একটা গতি যখন বারবার বিপরীত দিকে রিপিট হয় তখন তাকে বলা হয় পর্যাবৃত্ত গতি । পর্যাবৃত্ত গতি মানেই যে গতি একটা পর্যায়কে অনুসরণ করে । এর সবচেয়ে ভালো উদাহরণ একটা “পেন্ডুলাম” বা “সরল দোলক” । কোনো কিছুকে একটা সুতো দিয়ে ঝুলিয়ে দিয়ে সেটাকে একটু বাঁকিয়ে ছেড়ে দিলে দেখা যায় একবার ডানে আর একবার বামে যাবে । এভাবে একটা নির্দিষ্ট জিনিসকে অক্ষে রেখে একবার এদিক একবার ওদিক এই ধরনের গতিই পর্যাবৃত্ত গতি । একটা বৃত্তাকার গতির ক্ষেত্রেও বারবার তার পরিধির সব বিন্দুকে একটা নির্দিষ্ট সময় পর পর অতিক্রম করে । সেক্ষেত্রে এটাও পর্যাবৃত্ত গতি । তবে পদার্থবিজ্ঞানে সবচেয়ে সহজে বিষয়টা বুঝার জন্য আমরা পর্যাবৃত্ত গতির উদাহরণ হিসেবে সরল ছন্দিত স্পন্দনকেই নিয়ে থাকি ।

সরল ছন্দিত স্পন্দনঃ কোনো পর্যাবৃত্ত গতিসম্পন্ন বস্তুর বেগের দিক বারবার বিপরীতমুখী হলে এবং ত্বরণ সরণের সমানুপাতিক ও বিপরীতমুখী হলে তা সরল ছন্দিত স্পন্দন । নিচের চিত্রটা দেখুনঃ-

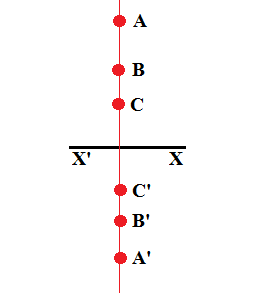
এখানে X’X যদি সাম্যাবস্থা হয়, তাহলে সরল ছন্দিত স্পন্দনের মধ্যবর্তী কোনো কণা (উপরের লাল কণা) আনুভূমিক অবস্থান ঠিক রেখেই উল্লম্বভাবে অবস্থানের পরিবর্তন করতে থাকে । অর্থাৎ, কোনো কণা বাম থেকে ডানে যায় না । বরং নিজের অবস্থানে থেকেই উপরে নিচে করতে থাকে । কণাটার বিস্তারে সর্বোচ্চ অবস্থান A এবং সর্বনিম্ন অবস্থান A’ দেখানো হয়েছে । এভাবে ক্ষুদ্রতম dt সময়ের ব্যবধান নিয়ে বারবার কণাটির অবস্থান (সাম্যাবস্থা থেকে দূরত্ব) নির্ণয় করলে আমরা নিচের মত একটা অবস্থান-সময় লেখ পাইঃ-

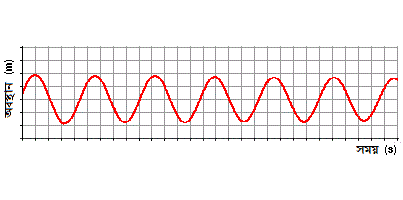
এটা একটা অবস্থান-সময় লেখ । এখানে কিন্তু লাল বক্ররেখা দিয়ে কোনো তরঙ্গ বুঝাচ্ছেনা । বরং সময়ের সাথে একটা কণার অবস্থান বুঝাচ্ছে । ফলে একটা লেখচিত্র পাওয়া যায় ।

এটা অনেকটা অভিকর্ষজ বলের মত কাজ করে । একটা বলকে সোজা উপরের দিকে ছুড়ে মারলে যেমন সর্বোচ্চ উচ্চতায় উঠলে বস্তুর গতি শূন্য হয় । আর সর্বনিম্ন উচ্চতায় বা ভূমিতে গতি সর্বোচ্চ হয় । ঠিক তেমনি সর্বোচ্চ অবস্থান তথা বিস্তারে কণার গতি সর্বনিম্ন হয় এবং সর্বনিম্ন অবস্থান তথা সাম্যাবস্থায় গতি সর্বোচ্চ হয় । সরল ছন্দিত স্পন্দনে বস্তুর এবং সাম্যাবস্থার মধ্যবর্তী দূরত্ব (s) জানলেই একে সময়ের সাপেক্ষে একবার ব্যবকলন করলে বেগ (v=ds/dt); প্রাপ্ত বেগকে সময়ের সাপেক্ষে আরেকবার ব্যবকলন করলে ত্বরণ (a=dv/dt); এবং প্রাপ্ত ত্বরণকে আরেকবার সময়ের সাপেক্ষে ব্যবকলন করলে যাতি (J=da/dt) পাওয়া যায় । সুতরাং, শুধু অবস্থান নির্ণয় করলেই আমরা গতির সব রাশির সমাধান করতে পারব । সরল ছন্দিত স্পন্দের ক্ষেত্রে অবস্থান নির্ণয়ের সমীকরণ হলঃ-

X=a sin (wt+d) [ফন্টের জন্য ওমেগাকে ডাব্লিউ এবং ডেলকে ডি দিয়ে প্রকাশ করা হয়েছে]

সূত্রটা কিভাবে আসলো তা যে কোনো উচ্চ মাধ্যমিক পদার্থবিজ্ঞান বইয়েই সবাই দেখতে পাবেন । ওটা আলোচনা করে আর্টিকেল দীর্ঘায়িত করব না ।

সুতরাং, কোনো বস্তুর অবস্থান জানতে হলে তার বিস্তার এবং দশা জানতে হবে । বিস্তার (a) এবং দশা (wt+d) জানলেই বস্তুর অবস্থান বের করা যাবে । এখানে, বিস্তার, কৌণিক বেগ (w) এবং আদি দশা (d) ধ্রুবক । শুধু সময় (t) পরিবর্তনশীল । পদার্থবিজ্ঞানের ভাষায়, উপরের সূত্রটিকে সময়ের সাপেক্ষে ব্যবকলনীয় সমীকরণের সমাধানও বলা হয় । অর্থাৎ, সময় এর ক্ষুদ্রতম পরিবর্তনের জন্য সরণের পরিবর্তনের জন্য উপরের সমীকরণ ব্যবহার করা যায় । ভার্চুয়াল রিয়েলিটিতে সময়ের ক্ষুদ্রাতিক্ষুদ্র পরিবর্তনকে লুপ (Loop) এর মাধ্যমে করা হয় । আর সময়ের সাপেক্ষে লুপ করতে সাধারণত প্রোগ্রামিং-এ টাইম ডেপেন্ডেন্ট রিকার্সিভ ফাংশন ইউজ করা হয় । আর জেকুয়েরীর সহায়তা নিলে আমরা বিষয়টা কলব্যাক ফাংশনের মাধ্যমে আরও সহজে করতে পারি ।

ওয়েব পেইজকে ভার্চুয়াল রেফারেন্স ফ্রেম (প্রসঙ্গ কাঠামো) হিসেবে বিবেচনা করলে জাভাস্ক্রিপ্টের মাধ্যমে আমরা উপরোক্ত সমীকরণের ভার্চুয়াল রিয়েলিটি দেখতে পারি ।

প্রথমে একটা ব্লাংক HTML পেজের মধ্যে নিচের কোড দিয়ে একটা প্রসঙ্গ কাঠামো তৈরী করব ।

<style>
.ball {width:20px;height:20px;position:absolute;left:50px;top:-10px;background:red;border-radius:10px;}
.line {width:120px;height:2px;position:absolute;left:20px;top:210px;background:black;}
.line:before {content:"X'";position:absolute;left:-15px;top:-10px;}
.line:after {content:"X";position:absolute;left:120px;top:-10px;}
</style>
<div class='line'><div class='ball'></div></div>

ফলে একটি অক্ষ এবং তার দু-পাশে দোলানোর জন্য প্রয়োজনীয় কণা তৈরী হয়ে গেল । এবার পেইজে জেকুয়েরী ইনক্লুড করে নিতে হবে । ধরা যাক সেটা করে ফেললাম । এবার প্রধাণ কাজ । জাভাস্ক্রিপ্ট অংশ । প্রথমে ধ্রুবকগুলো জাভাস্ক্রিপ্টে এমবেড করে নিই । এসব মান এই স্পন্দনের ক্ষেত্রে ধ্রুবক ধরা যাক ।

var ball=$(".ball"),
t     =0,
a     =100,
Wd    =10,
Wr    =(Math.PI*Wd)/180, W=Wr;

যেহেতু স্পন্দনের সময়কে শূন্য থেকে অসীমের মধ্যে ব্যবকলন করা হয় । তাই আমরা লুপের ক্ষেত্রে সময়ের প্রারম্ভ শূন্য ধরেছি; সেই সাথে বিস্তার ১০০ পিক্সেল (কম্পিউটারে দৈর্ঘ্যের একক পিক্সেল) এবং কৌণিক বেগ ১০ ডিগ্রী ধরে পরে তা হিসেবের সুবিধার জন্য রেডিয়ানে রুপান্তর করেছি । এই পর্যন্ত কাজ এতোটুকুই । এবার আমরা রিকার্সিভ ফাংশনটা লিখব ।

function run(){
t+=1;
WT=W*t;
y=a * Math.sin(WT); // The equation of simple harmonic Oscillation
topNew=y;
ball.animate({top:topNew},50,"linear",function(){run();});
}

রান ফাংশনটিতে, প্রথমে সময়কে এক এক করে বাড়ানো হয় এবং প্রতিক্ষেত্রে y=a sin(wt) [because, d=0] সূত্র দিয়ে তার অবস্থান নির্ণয় করা হয় । তারপর সেটাকে তার নতুন অবস্থান হিসেবে রূপ দিতে জেকুয়েরীর animate অবজেক্টকে কল করা হয় । এখানে আবার কলব্যাকের মাধ্যমে এই ফাংশনকেই উল্লেখ করে রিকার্সন করা হয় । যেহেতু সময় অসীম পর্যন্ত হয় তাই এখানে রিকার্সনের কোনো সীমাবদ্ধতা দেয়া হয়নি । পেজ লোড হয়ে গেলে অসীম সময় ধরে এই ফাংশন কাজ করতেই থাকবে ।

সবশেষে, আমাদের ফলাফল হয়ঃ সরল ছন্দিত স্পন্দনের ভার্চুয়াল রিয়েলিটি

তরঙ্গ হল সরল ছন্দিত স্পন্দনেরই যৌথ রুপ । তরঙ্গ বলতে এমন একটি প্রক্রিয়াকে বুঝি যে প্রক্রিয়ায় কোনো মাধ্যমের এক প্রান্ত থেকে অন্য প্রান্তে শক্তি স্থানান্তরিত হয় কণাগুলোর সরল ছন্দিত স্পন্দনের মাধ্যমেই । অর্থাৎ, তরঙ্গের মধ্যে বস্তুগুলোর আনুভূমিক সরণ শূন্য থাকে, কণাগুলো শুধু উপরে নিচে সরল ছন্দিত গতিতে দুলতে দুলতে মাধ্যমের এক প্রান্ত থেকে অন্য প্রান্তে শক্তি ও তথ্য স্থানান্তরিত করে । এর সবচেয়ে সাধারণ ও উৎকৃষ্ট উদাহরণ হতে পারে পানির ঢেউ বা স্রোত । অথবা, একটা সুতোকে একপ্রান্তে ধরে সামান্য দুলিয়ে ছেড়ে দিলে দেখা যায় সুতো আপনার হাতেই আছে কিন্তু একটা তরঙ্গ খেলে যায় তার এক প্রান্ত থেকে অপর প্রান্তে । এভাবে শক্তি সঞ্চালিত হয় ।

এখানে পরমাণুবাদের ধারণা বর্ণনা করা যেতে পারে । জগতের প্রতিটি জিনিসই ছোট ছোট কণা দিয়ে গঠিত যাদের পরমাণু বলা হয় । তেমনি, পৃথিবীর সকল ঘটনাই আপেক্ষিক । আপনি বিছানা থেকে বাথরুমে গেলেন । বিষয়টা সাধারণভাবে দেখলে দেখা যাবে যে আপনি বিছানা থেকে উঠে বাথরুমে গেলেন । কিন্তু ক্যালকুলাস এবং পদার্থবিজ্ঞান দিয়ে দেখলে আমরা দেখব, সময়ের পরিবর্তনের সাথে আপনার অবস্থানের পরিবর্তন ঘটল, অর্থাৎ সরণ হল । একটু সময় অতিবাহিত হওয়ার সাথে সাথে আপনি এক জায়গা থেকে অন্য জায়গায় গেলেন । ধরা যাক, বিছানা থেকে বাথরুমে যেতে আপনার সময় লাগলো ১০ সেকেন্ড আর বিছানা থেকে আপনার বাথরুমের দূরত্ব ১০ মিটার । ফলে, যখন আপনি বিছানায় শুয়ে ছিলেন তখন থেকে ১০ সেকেন্ড পর আপনি ১০ মিটার দূরে অবস্থিত বাথরুমে বসে ছিলেন । কিন্তু এই ১০ সেকেন্ড পর কি আপনি চোখের পলকে বিছানা থেকে বাথরুমে চলে গিয়েছেন? না, বরং একটু একটু করে গিয়েছেন । প্রথমে ১ সেকেন্ডে গিয়েছেন ১ মিটার দূরে । তারপরের ১ সেকেন্ডে গিয়েছেন আরও এক মিটার দূরে । এভাবে মোট ১০ সেকেন্ড সময় পর গিয়েছেন ১০ মিটার দূরে । অর্থাৎ, অল্প অল্প সময় পর পর আপনার অবস্থানেরও অল্প অল্প পরিবর্তন হয়েছে । এই ধারণাটাই ক্যালকুলাসের প্রতিষ্ঠার পেছনে কাজ করেছিলো । নিউটন দেখলেন, প্রত্যেকটা ঘটনাই ছোট ছোট কিছু ঘটনার সমষ্টি । তেমনিভাবে প্রত্যেকটা পরিবর্তনই ছোট ছোট কিছু পরিবর্তনের সমষ্টি । উপরের উদাহরনে যেমন দেখলাম, অল্প কিছু সময় পরপর অল্প কিছু দুরত্ব অতিক্রম করে করে শেষ পর্যন্ত কিছু সময় পর আপনি আপনার গন্তব্যে পৌঁছালেন । অর্থাৎ, সময়ের ক্ষুদ্রতম (সবচেয়ে ক্ষুদ্র) পরিবর্তনে আপনার অবস্থানেরও সামান্য পরিবর্তন ঘটেছে । এভাবে অনেকগুলো সময়ের পরিবর্তনের সমষ্টি দিয়ে আপনার অবস্থানের পরিবর্তন করেই আপনি বাথরুমে পৌঁছালেন । এই বিষয়টাকেই ক্যালকুলাস বলা হয় ।

ক্যালকুলাসের দুইটা অংশ, অন্তরীকরণ এবং যোগজীকরণ । অন্তরীকরণ আমাদের কোনো জিনিসের ক্ষুদ্রতম পরিবর্তনের ফলে তার উপর নির্ভরশীল অন্য জিনিসের পরিবর্তন দেখায় । যেমন উপরের উদাহরণে সময়ের ক্ষুদ্রতম পরিবর্তনে (১ সেকেন্ডে) আপনার অবস্থানেরও সামান্য পরিবর্তন (১ মিটার) ঘটেছে । আর যোগজীকরণ একটা ঘটনার ক্ষেত্রে কোনো বস্তুর মোট পরিবর্তনের সাথে তার উপর নির্ভরশীল অন্য বস্তুর মোট পরিবর্তন হিসেব করতে সাহায্য করে । যেমন উপরের উদাহরণে মোট ১০ সেকেন্ড সময় পর আপনার মোট অবস্থানের পরিবর্তন হয়েছে ১০ মিটার । এইটাই ক্যালকুলাস ।

সবচেয়ে মজার (অথবা বাজে) ব্যাপার হল, লজিকাল সব কাজ করতেই প্রোগ্রামিং এ ক্যালকুলাস ব্যবহার করতে হয় । কারণ ক্যালকুলাসই কিছু লজিকের সমষ্টি । উপরে সরল ছন্দিত স্পন্দন দেখিয়েছি, সেটাতেও এলগরিদম করতে আমাকে ক্যালকুলাসের সাহায্য নিতে হয়েছে । একটু ভালোমত উপরের run() ফাংশনটা দেখলেই বুঝবেন ওখানে সময়ের সামান্য পরিবর্তনের সাপেক্ষে কণাটির অবস্থানের পরিবর্তন ঘটিয়েছি এবং এই প্রক্রিয়াটা ফাংশন রিকার্সনের মাধ্যমে বারবার ঘটিয়েছি । এবং এক্ষেত্রে সীমা দিয়েছি পেজ লোড হতে শুরু করে অসীম পর্যন্ত । ফলে সারা জীবন ধরে উপরের উদাহরণে কণাটা সরল ছন্দিত স্পন্দন দেখাতেই থাকবে ।

আগেই বলেছি, তরঙ্গ মানেই অনেকগুলো সরল ছন্দিত স্পন্দনে স্পন্দনশীল কণার সমষ্টি । যদিও ভালো ফলাফলের জন্য তরঙ্গ বিষয়টার এক্সপেরিমেন্ট অন্য পদ্ধতিতে করাই শ্রেয়, তবে আমি উপরের সরল ছন্দিত স্পন্দনের বিষয়টাকেই বেছে নিলাম । এতে করে তরঙ্গ যে সরল ছন্দিত স্পন্দনেরই সম্মিলিত রুপ তা প্রমাণিত হবে ।

প্রথমে উপরের কোডগুলো সামান্য পরিবর্তন করতে হবে । কারণ, উপরে একটা ফাংশন দিয়ে শুধু একটা কণাকেই ব্যবহার করেছি । কিন্তু এবার অসংখ্য কণাকে এই একটা ফাংশনের মাধ্যমেই কাজ করাব । তাই সামান্য পরিবর্তন ।

সিএসএসঃ-

.ball {width:20px;height:20px;position:absolute;left:0px;top:-10px;background:red;border-radius:10px;}
.line {width:200px;height:2px;position:absolute;left:20px;top:210px;background:white;}

এইচটিএমএলঃ-

<div class='line'>
<script>for (i=0;i<=50;i++){document.write("<div class='ball ball"+i+"' style='left:"+(i*20)+"px;top:-10px;'></div>");}</script>
</div>

এখানে দেখুন, line ডিভ এর মধ্যে জাভাস্ক্রিপ্ট এর মাধ্যমে লুপিং করে ৫০ টা কণাকে একসাথে পাশাপাশি নিয়েছি । এবার তাদের সবাইকেই নির্দিষ্ট সময় সাপেক্ষে ওই ফাংশনের মধ্য দিয়ে নিয়ে যাব ।

এবার জাভাস্ক্রিপ্ট কোডেও সামান্য পরিবর্তন হবে । ডিফল্ট ভেরিয়েবলগুলো হলঃ-

var a=100,
Wd=10,
speed=100,
Wr    =(Math.PI*Wd)/180, W=Wr;

তরঙ্গের ক্ষেত্রে প্রত্যেকটা কণার দশা আলাদা হবে । তাই তাদের সময়ের ব্যবধানও আলাদা হবে । তাই, প্রত্যেকটা কণার জন্য আলাদা আলাদা সময় নির্ধারণ করতে নিচের কোড লিখবঃ-

var time= new Array();
for (j=0;j<=document.getElementsByClassName("ball").length;j++){time[j]=0;}

এবার আগের ফাংশনটাই প্রত্যেকটা সময়ের জন্য সামান্য মডিফাই করে নিচের মত করে লিখবঃ-

function run(particle){
ball=$(particle);
number = particle.substr(5);
time[number]+=speed/100;
t=time[number];
WT=W*t;
y=a * Math.sin(WT);
topNew=y-10;
$(particle).animate({top:topNew},100,"linear",function(){run(particle);});
}

এবার সবগুলো কণাকে নির্দিষ্ট সময়ের ব্যবধানে কল করলেই হয়ে যাবে আমাদের প্রোগ্রাম । আরও কিছু কোড দিয়ে একটা সম্পূর্ণ এইচটিএমএল ফাইল তৈরী করে কল করলেই হয়ে যাবে তরঙ্গের ভার্চুয়াল রিয়েলিটি ।

সবশেষে আমাদের ফলাফল হয়ঃ তরঙ্গের ভার্চুয়াল রিয়েলিটি

একটা বস্তুকে কোনো কিছুর সাথে বেঁধে একদিকে টেনে ছেড়ে দিলে সেটা দুলতে থাকে । যেমনঃ দোলনা । দোলনার ক্ষেত্রে দেখা যায়, এটাকে পিছন দিকে টেনে ছেড়ে দিলে সামনে পেছনে দুলতে থাকে । ফলে তৈরী হয় একটা দোলক । অর্থাৎ, জগতের যা কিছুই সামনে পেছনে কিংবা ডানে বামে দুলতে থাকে তাকেই দোলক বলা হয় ।

সরল দোলকঃ হালকা নমনীয় সুতার সাথে ঝুলে থেকে ওজনহীন কোনো বস্তুকে অল্প একটু ডানে/বামে সরিয়ে ছেড়ে দিলে তা সরল ছন্দিত গতিতে দুলতে থাকে । এটাই সরল দোলক ।

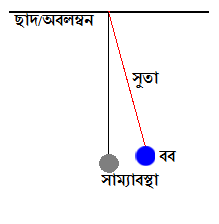
উপরের চিত্রটা দেখুন । একটা ববকে ছাদের সাথে ঝুলিয়ে রাখা হয়েছে । এটাকে সাম্যাবস্থা থেকে কিছু দূরে টেনে ছেড়ে দিয়ে তৈরী হয়েছে একটা সরল দোলক । এই সরল দোলকের গতি এক প্রকার পর্যাবৃত্ত গতি এবং এটি সরল ছন্দিত গতিকেও সমর্থন করে ।

সরল দোলকের গতি হল একটা জটিল প্রকারের পর্যাবৃত্ত গতি । কারণ, এক্ষেত্রে ববের দ্বিমাত্রিক সরণ হয় । ববটি উপরে নিচেও ওঠানামা করে, আবার ডানে বামেও যায় । তাই এর গতিয় অবস্থা নিয়ে কাজ করতে আমাদের সামান্য জটিলতার সম্মুখীন হতে হয় । একটা নির্দিষ্ট সময় পর ববটির অবস্থান কোথায় হবে তা নির্ণয় করতে হলে আমাদের তার আনুভূমিক এবং উল্লম্ব উভয় অবস্থানই নির্ণয় করতে হবে । এটি নির্ণয় করার জন্য সবচেয়ে জটিল এবং সবচেয়ে সহজ দুই প্রকার পদ্ধতিই ব্যবহার করা যায় । সবচেয়ে জটিল পদ্ধতির সামান্য ধারণা দেব এবং সহজ পদ্ধতিটা নিয়েই আজকের এক্সপেরিমেন্ট করব ।

জটিল পদ্ধতিঃ এক্ষেত্রে ববটির অবস্থান দ্বিমাত্রিক গতিবিদ্যার মাধ্যমে নির্ণয় করতে হয় । সাম্যাবস্থায় বস্তুটির উপর প্রযুক্ত নীট বল শূন্য হয় । কারণ ববের ওজন এবং সূতার বিপরীতমুখী সমান বলের ফলে মোট কাজ শূন্য । কিন্তু ববটিকে একটু টেনে ছেড়ে দিলে প্রথম অবস্থায় তার ওজনের একটা অংশ (mg cosA) সুতোর সাথে লম্বভাবে কাজ করে এবং তা সুতোর সমান ও বিপরীতমুখী প্রতিক্রিয়ার ফলে শূন্য হয়ে যায় । আর ওজনের বাকী অংশ (mg sinA) সাম্যাবস্থার দিকে প্রথমে A কোণে ক্রিয়া করে । ফলে একটা সাম্যাবস্থা অভিমুখী ত্বরণ (a=-gsinA) তৈরী হয় । এই ত্বরণের ফলেই ববটি সাম্যাবস্থার দিকে আসে । সময়ের অতিক্ষুদ্র ব্যবধানে অন্তরীকরণ করলে এই ত্বরণের আনুভূমিক এবং উল্লম্ব উপাংশদ্বয় থেকে তার পরমুহূর্তের অবস্থান পাওয়া যায় । কিন্ত সর্বাধিক উচ্চতা এবং সাম্যাবস্থার মাঝামাঝি যে কোনো অবস্থানে বস্তুটির গতিশক্তি এবং স্থিতিশক্তি উভয়ই কার্যকর থাকে । তাই তার গতি এবং অভিকর্ষজ ত্বরণের যৌথ ক্রিয়ায় ববটি যতোই সাম্যাবস্থানের দিকে যায় তার বেগ ততই বাড়তে থাকে । কিন্তু ত্বরণের সমীকরণ  a=-gsinA এর ক্ষেত্রে A (সাম্যাবস্থার সাথে সুতোর উৎপন্ন কোণ) সময়ের সাপেক্ষে পরিবর্তনশীল । ফলে ত্বরণও পরিবর্তনশীল । এভাবে অতি ক্ষুদ্র সময়ের ব্যবধানে বারবার অন্তরীকরণ করে ক্যালকুলাস ব্যবহার করে ববের অবস্থান পাওয়া যায় । এটা সবচেয়ে জটিল পদ্ধতি ।

সহজ পদ্ধতিঃ ভাবুন তো, ববের আনুভূমিক আর উল্লম্ব সরণের মধ্যে কি কোনো সম্পর্ক আছে? ববের কোণের সাথেই বা তার আনুভূমিক আর উল্লম্ব সরণের সম্পর্ক কী?

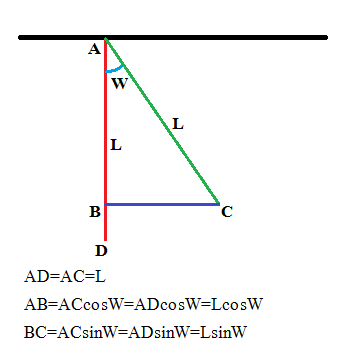
উপরের চিত্রটা দেখুন । সুতো যেখানে বাঁধা হয়েছে সেখান থেকে ববের অবস্থানের দৈর্ঘ্য সবসময় একই । সাম্যাবস্থায় ববটা D অবস্থানে এবং একটু ডানে সরিয়ে ববকে C অবস্থানে আনা হলেও এর কার্যকরী দৈর্ঘ্য L=AD=AC সবসময় নির্দিষ্ট থাকে । তাই সাম্যাবস্থান থেকে তার আনুভূমিক এবং উল্লম্ব উভয় সরণকেই তো এর মাধ্যমে প্রকাশ করা যায় । উপরের চিত্রে, যদি ববটি C অবস্থানে থাকে তাহলে মূলবিন্দু থেকে তার অবস্থানের পার্থক্য হবে BD এবং BC । BD=AD-AB লেখা যায় । এখন, তার কোণ W জানা থাকলে ত্রিকোণোমিতি থেকে আমরা এর আনুভূমিক এবং উল্লম্ব সরণ বের করতে পারিঃ-
AB = LcosW
BC = LsinW

উভয় সমীকরণে শুধু W এর মান পরিবর্তনশীল, কিন্তু L ধ্রুবক । তার মানে, তার কোণ জানলেই অবস্থান জানা যায় । এই সহজ সমীকরণদ্বয় থেকেই আমরা ববটির অবস্থানের প্রোগ্রাম বানাবো । তো চলুন শুরু করা যাক ।

আর যেহেতু এটা সরল ছন্দিত গতি, তাই তার কৌণিক অবস্থানের সমীকরণ হলঃ-

A=Ao cos(wt) [Ao=Starting Angle, w=Angular Velocity, t=time]

এবারও আমরা প্রথমে একটা ফাঁকা ওয়েবপেইজ নেব ।

<!doctype html><html lang=”en”><head><meta charset=”utf-8” /></head><body></body></html>

ছাদ, সূতার আদিবিন্দু এবং বব তৈরী করি ।

<div class="frame">
<div class="mainPoint">
<div class="lineY"></div>
<div class="bob"></div>
</div>
</div>

এগুলোর সিএসএসঃ-

.frame {position:absolute;top:50px;left:100px;background:black;width:200px;height:2px;}
.mainPoint {position:absolute;background:red;width:2px;height:2px;left:99px;top:0px;}
.bob {width:20px;height:20px;border-radius:10px;background:blue;position:absolute;top:150px;left:0px;}
.lineY {background:red;width:1px;position:absolute;}

ব্যস, একটা সরল দোলক তৈরী হয়ে গেল । এবার এটাকে কার্যকর করব জাভাস্ক্রিপ্টের মাধ্যমে ।

প্রথমে এর প্রোপার্টিগুলোর মান জানিয়ে দিই কম্পিউটারকেঃ-

var Amax=30, bob = $(".bob"), W=1.2, t=0, L=150, speed=100;

এখানে, W দিয়ে কৌণিক বেগ এবং L দিয়ে কার্যকরী দৈর্ঘ্য এবং Amax দিয়ে আদি অবস্থান (কৌণিক) বুঝানো হয়েছে ।

এবারে আদি অবস্থানে ববটিকে নিয়ে আসিঃ-

function rad(Angle){//Converts Degree unit to Radian
return (Math.PI*Angle)/180;
}
function arad(Angle){//Converts Radian unit to Degree
return (180*Angle)/Math.PI;
}
function rope(Angle){
elem=$(".lineY");
Angle=-Angle;
l=L/2;
postop=-l+(l*Math.cos(rad(Angle)))+2;
left=-(l*Math.sin(rad(Angle)));
elem.css({"transform":"rotate("+Angle+"deg)","left":left,"top":postop});
}

উপরের শেষ ফাংশনটি দড়ির অবস্থানকে নির্দেশ করে । এটা সিএসএস৩ রোটেট ইফেক্ট ইউজ করায় বাগ ফিক্সিং হিসেবে নেওয়া যায় ।

X=L*Math.sin(rad(Amax));
Y=L*Math.cos(rad(Amax));
repos(X,Y);
rope(Amax);
$(".lineY").css("height",L);
function repos(posX,posY){//Moves the bob
bob.css({"left":posX-10,"top":posY-10});
}

এই কোডগুলো এর কোণ অনুযায়ী ববটিকে নির্দিষ্ট অবস্থানে নিয়ে যায় ।

function run(){
t+=speed/100; //Set's time interval
WT=W*t; //Counts (W*t)
A=Amax * Math.cos(rad(WT)); //Defined as: A=Amax*(Wt+d); Here, d=0
//console.log(A);
X=L*Math.sin(rad(A)); //Vertical position of the bob
Y=L*Math.cos(rad(A)); //Horizontal position of the bob
rope(A);
bob.animate({left:X-10,top:Y-10},10,"linear",function(){run();}); //Moves the bob and makes infinite loop
}
run();

এই ফাংশনটাই প্রধান ফাংশন । এটি কৌণিক অবস্থান নির্ণয় করে বস্তুটির আনুভূমিক এবং উল্লম্ব অবস্থান নির্ণয় করে এবং একইসাথে ববটিকে সেই অবস্থানে নিয়ে যায় । ব্যস, তৈরী হয়ে গেল আমাদের ভার্চুয়াল রিয়েলিটি । এবার প্রোগ্রামটিকে রান করালে আমরা একটা সরল দোলক দেখতে পাব ।

এই প্রোগ্রামটাকেই আরেকটু সমৃদ্ধ করলে চুড়ান্ত ফলাফল পাওয়া যায় ।

সবশেষে আমাদের ফলাফল হয়ঃ সরল দোলকের ভার্চুয়াল রিয়েলিটি

বাংলাদেশ থেকে পৃথিবীর কেন্দ্র দিয়ে আমেরিকা পর্যন্ত আপনি একটা সোজা সুড়ঙ্গ খুঁড়লেন । তারপর সেটাতে লাফ দিলেন । সেক্ষেত্রে আপনার ভবিষ্যত কি হবে? নিচের উত্তরগুলোর মধ্যে সঠিক উত্তর কোনটি? (বাতাসের বাধা উপেক্ষনীয়)

১) পৃথিবীর কেন্দ্রে গিয়ে থেমে যাবেন

২) সোজা আমেরিকা চলে গিয়ে থেমে যাবেন

৩) সুড়ঙ্গের এক প্রান্ত থেকে অপর প্রান্তে যাওয়া আসা করবেন

৪) সরল দোলন গতিতে চলতে চলতে একসময় কেন্দ্রে গিয়ে থেমে যাবেন

আপনার উত্তরটি সঠিক কিনা ভার্চুয়াল রিয়েলিটির মাধ্যমে প্রমাণ করতে হবে । আপনার পছন্দমত যে কোনো প্রোগ্রামিং ল্যাঙ্গুয়েজ দিয়েই করতে পারেন । এবং অবশ্যই উপরের এক্সপেরিমেন্টগুলোর মত পদার্থবিজ্ঞানের সূত্র দিয়েই সব করতে হবে । উত্তরসহ আমাকে মেইল অথবা ফেসবুকে মেসেজ করতে পারেন । যিনি সঠিক উত্তরের সাথে ভার্চুয়াল রিয়েলিটির প্রোগ্রামটা সঠিকভাবে করে দেখাতে পারবেন তার জন্য রয়েছে আকর্ষণীয় পুরষ্কার । এছাড়াও যে কোনো মন্তব্য, উপদেশ বা জিজ্ঞাসা নিয়েও আমার সাথে যোগাযোগ করতে পারেন ।

• ফেসবুকঃ http://www.facebook.com/arif.reza.rifat
• ইমেইলঃ [email protected]

আমাদের চারপাশের জগতটা যতো কঠিন, ততোই মজার । এই আনন্দ নিতে হলে প্রয়োজন ইচ্ছের । ইচ্ছের চেয়ে বড় শক্তি পৃথিবীতে নেই । পদার্থবিজ্ঞানের জগতটাও আমরা যেমন ভাবি তেমন জটিল আর সমীকরণে ভরপুর নয় । এখানেও আছে যথাযথ আনন্দের উৎস । শুধু পরীক্ষার জন্য নয়, কিছু জানার জন্য লেখাপড়া করতে হবে । তাহলে দেখবেন আপনার পাঠ্যবইয়ের চেয়ে আনন্দদায়ক আর কোনো কিছুই পৃথিবীতে নেই । সবাইকে অসংখ্য ধন্যবাদ জানিয়ে আজকের আর্টিকেল শেষ করছি । আসসালামু আলাইকুম ।