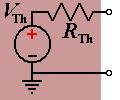
[পর্ব-১|পর্ব-২|পর্ব-৩|পর্ব-৪|পর্ব-৫] আজকের পর্বে থেভেনিন'স ও নর্টন'স থিয়রেম এবং তাদের প্রয়োগ নিয়ে আলোচনা করা হবে। ইলেকট্রিক সার্কিট বিশ্লেষণের জন্য থেভেনিন'স থিয়রেম একটি খুবই গুরুত্বপূর্ণ ও প্রয়োজনীয় থিয়রেম। পাওয়ার সিস্টেমের ক্ষেত্রে এই থিয়রেম বিশেষ ভাবে ব্যবহার করা হয়। থেভেনিন'স থিয়রেম অনুযায়ী একাধিক সোর্স ও রোধকের সমন্বয়ে গঠিত যে কোন দুই-টার্মিনাল বিশিষ্ট লিনিয়ার সার্কিটকে একটি ভোল্টেজ সোর্স ও একটি সিরিজ রোধক দ্বারা প্রতিস্থাপন করা যায়। নিচের ডায়াগ্রামটি লক্ষণীয় যেখানে বাম পাশের ব্ল্যাক বক্সের মধ্যে একাধিক ভোল্টেজ সোর্স, একাধিক কারেন্ট সোর্স, ও একাধিক রোধক আছে। ব্ল্যাক বক্সের মধ্যে জটিল সার্কিটকে একটি ভোল্টেজ সোর্স ও একটি সিরিজ রোধক দ্বারা প্রতিস্থাপন করা হয়েছে, ডান পাশের সার্কিট লক্ষণীয়। ডান পাশের সরল সার্কিটকে মূল সার্কিটের থেভেনিন-সমতুল্য সার্কিটও বলা হয়।
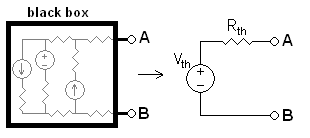
দুই-টার্মিনাল বিশিষ্ট যে কোন জটিল সার্কিটের থেভেনিন-সমতুল্য সার্কিট (Rth ও Vth) পেতে হলে নিম্নের ধাপগুলো অনুসরণ করতে হবে:
ধাপ-১: সবগুলো ভোল্টেজ ও কারেন্ট সোর্সকে নিষ্ক্রিয় করে টার্মিনাল A ও B এর মধ্যে তুল্য রোধ বের করতে হবে। এই তুল্য রোধই হচ্ছে Rth. Rth কে থেভেনিন-সমতুল্য রোধও বলা হয়। এই পদ্ধতি শুধুমাত্র ইনডিপেনডেন্ট সোর্স এর ক্ষেত্রেই প্রযোজ্য।
ধাপ-২: মূল সার্কিটে টার্মিনাল A ও B এর মধ্যে কোন রোধক থাকলে সেটিকে খুলে ফেলে যে কোন পদ্ধতির সাহায্যে A ও B এর মধ্যে ভোল্টেজ নির্ণয় করতে হবে। A ও B এর মধ্যে ভোল্টেজই হবে Vth, যাকে ওপেন-সার্কিট ভোল্টেজও বলা হয়।
ধাপ-৩: Rth ও Vth এর মান পাওয়ার পর থেভেনিন-সমতুল্য সার্কিট আঁকতে হবে। উপরের ডায়াগ্রামে ডান পাশের সার্কিট দ্রষ্টব্য।
উল্লেখ্য যে, ধাপ ১ ও ২ একে-অপর থেকে স্বতন্ত্র। ফলে যে কোনটি আগে সম্পন্ন করা যায়। এবার একটি উদাহরণ দেয়া যাক। নিচের সার্কিটে একটি ভোল্টেজ সোর্স ও চারটি রোধক আছে। টার্মিনাল A ও B এর মধ্যে থেভেনিন-সমতুল্য সার্কিট বের করতে হবে।
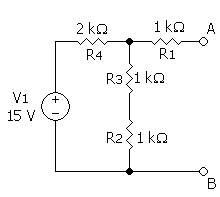
ধাপ-১ অনুযায়ী ভোল্টেজ সোর্সকে নিষ্ক্রিয় করলে নিচের সার্কিট পাওয়া যাবে। এই সার্কিটে টার্মিনাল A ও B এর মধ্যে তুল্য রোধের মান হবে, RAB = Rth = R1 + [(R2 + R3)||R4] = 1 + [(1 + 1)||2] = 2 kΩ.

ধাপ-২ অনুযায়ী মূল সার্কিটে টার্মিনাল A ও B এর মধ্যে ভোল্টেজ হবে, VAB = Vth = V1 (R2 + R3)/(R2 + R3 + R4) = 15 (1 + 1)/(1 + 1 + 2) = 7.5 V. উল্লেখ্য যে, টার্মিনাল A ও B যেহেতু ওপেন সেহেতু রোধক R1 এর মধ্যে দিয়ে প্রবাহিত কারেন্ট হবে শূন্য; ফলে R1 এর আড়াআড়ি বিভব পার্থক্যও শূন্য হবে।

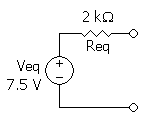
Rth ও Vth এর মান পাওয়ার পর নিচের মতো করে থেভেনিন-সমতুল্য সার্কিট আঁকতে হবে। মূল সার্কিটে টার্মিনাল A ও B এর মধ্যে কোন রোধক খুলে থাকলে সেটিকে এখানে পুনরায় যুক্ত করতে হবে।
নর্টন'স থিয়রেম: নর্টন'স থিয়রেম অনুযায়ী একাধিক সোর্স ও রোধকের সমন্বয়ে গঠিত যে কোন দুই-টার্মিনাল বিশিষ্ট লিনিয়ার সার্কিটকে একটি কারেন্ট সোর্স ও একটি সমান্তরাল রোধক দ্বারা প্রতিস্থাপন করা যায়। নিচের ডায়াগ্রামে বাম পাশের ব্ল্যাক বক্সের মধ্যে একটি জটিল সার্কিট ও ডান পাশে সেটির নর্টন-সমতুল্য সার্কিট দেখানো হয়েছে।

এখানে RNo হচ্ছে নর্টন-সমতুল্য রোধ এবং INo হচ্ছে নর্টন-সমতুল্য কারেন্ট। নর্টন-সমতুল্য সার্কিট দু-ভাবে পাওয়া যেতে পারে। ইতোমধ্যে যদি থেভেনিন-সমতুল্য সার্কিট জানা থাকে তাহলে খুব সহজেই সোর্স রূপান্তরের সাহায্যে নর্টন-সমতুল্য সার্কিট পাওয়া যায়, এবং বিপরীতটাও সত্য। এজন্য থেভেনিন-সমতুল্য সার্কিট ও নর্টন-সমতুল্য সার্কিটকে একে-অপরের সমতুল্য বলা হয়। সম্পর্কগুলো নিম্নরূপ,
Rth = RNo
INo = Vth/Rth
Vth = INo RNo
উপরে বাম পাশের সার্কিটকে নর্টন-সমতুল্য সার্কিট এবং ডান পাশেরটিকে থেভেনিন-সমতুল্য সার্কিট বলা হয়। স্বতন্ত্র পদ্ধতিতেও নর্টন-সমতুল্য সার্কিট পাওয়া যায়। যেমন Rth ও RNo বের করার পদ্ধতি একই এবং প্রকৃতপক্ষে Rth = RNo. অন্যদিকে নর্টন-সমতুল্য কারেন্ট INo পেতে হলে টার্মিনাল A ও B কে শর্ট সার্কিট করে যে কোন পদ্ধতির সাহায্যে A ও B এর মধ্যে কারেন্ট বের করতে হবে। এই কারেন্টই হবে INo, যাকে শর্ট-সার্কিট কারেন্টও বলা হয়। RNo ও INo এর মান পাওয়ার পর উপরে বাম পাশের সার্কিটের মতো করে নর্টন-সমতুল্য সার্কিট আঁকতে হবে।
আমি এস. এম. রায়হান। বিশ্বের সর্ববৃহৎ বিজ্ঞান ও প্রযুক্তির সৌশল নেটওয়ার্ক - টেকটিউনস এ আমি 14 বছর 6 মাস যাবৎ যুক্ত আছি। টেকটিউনস আমি এ পর্যন্ত 27 টি টিউন ও 123 টি টিউমেন্ট করেছি। টেকটিউনসে আমার 1 ফলোয়ার আছে এবং আমি টেকটিউনসে 0 টিউনারকে ফলো করি।
সার্কিট ডায়াগ্রামগুলো ফ্রী নেট থেকে নেয়া হয়েছে।
এই সিরিজের এটাই শেষ টিউন! ধৈর্যে আর কুলায় না। সিরিজটির দ্বারা সামান্যতমও কারো উপকার হলে আমার পরিশ্রম স্বার্থক হবে।
সাথে থাকার জন্য সবাইকে ধন্যবাদ।