[পর্ব-১] গত পর্বে সিরিজ, সমান্তরাল, এবং ওয়াই-ডেল্টা সংযোগ নিয়ে সংক্ষেপে আলোচনা করা হয়েছে। এই পর্বে সার্কিট বিশ্লেষণের আরো একটি মৌলিক বিষয়, কার্শহফ'স সার্কিট নীতি (Kirchhoff's Circuit Laws) নিয়ে আলোচনা করা হবে। কার্শহফ'স সার্কিট নীতি আসলে দুটি: কার্শহফ'স কারেন্ট নীতি (Kirchhoff's Current Law) এবং কার্শহফ'স ভোল্টেজ নীতি (Kirchhoff's Voltage Law)। এই দুটি নীতিই শক্তির নিত্যতা সূত্রের উপর ভিত্তি করে প্রতিষ্ঠিত। নীতি দুটি নিয়ে আলোচনাতে যাওয়ার আগে সংযোগস্থল বা নোড (Node/Junction) এবং ফাঁস বা লুপ (Loop) সম্পর্কে ধারণা থাকতে হবে। সাধারণ অর্থে দুই বা ততোধিক ব্র্যাঞ্চ এর মিলিত সংযোগস্থলকে নোড বলা হয়, তবে সার্কিট বিশ্লেষণের ক্ষেত্রে তিন বা ততোধিক ব্র্যাঞ্চ এর মিলিত সংযোগস্থল বিবেচনা করা হয়ে থাকে যাকে বলে এসেনশিয়াল নোড (Essential Node)। অর্থাৎ নোড হচ্ছে একটি বিন্দু বা সংযোগস্থল যেখানে দুই বা ততোধিক ব্র্যাঞ্চ মিলিত হয়। অন্যদিকে ফাঁস বা লুপ হচ্ছে বৃত্তের মতো বদ্ধ পথ।

কার্শহফ'স কারেন্ট নীতি (KCL): এই নীতি অনুযায়ী কোন নোড বা বিন্দুতে যে পরিমাণ কারেন্ট প্রবেশ করে, ঠিক একই পরিমাণ কারেন্ট সেই বিন্দু থেকে বেরিয়ে যায়। অন্যভাবে বললে বলা যায়, কোন বিন্দুতে কারেন্ট এর বীজগণিতীয় যোগফল শূন্য। বীজগণিতীয় যোগফল বলা হচ্ছে এ কারণে যে, কারেন্ট ধনাত্মক বা ঋণাত্মক হতে পারে। যেমন একটি বিন্দুতে কারেন্ট এর প্রবেশকে যদি ধনাত্মক ধরা হয় তাহলে সেই বিন্দু থেকে কারেন্ট এর বহির্গমনকে ঋণাত্মক ধরতে হবে, এবং এর বিপরীতটাও সত্য। গণিতের সাহায্যে কার্শহফ'স কারেন্ট নীতিকে নিম্নের সমীকরণ দ্বারা প্রকাশ করা যায়,

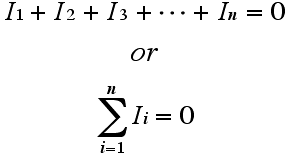
যেখানে n হচ্ছে একটি বিন্দুতে সংযুক্ত মোট ব্র্যাঞ্চের সংখ্যা। এবার নিচের চিত্রটি লক্ষ্য করা যাক। চিত্র অনুযায়ী একটি বিন্দুতে চারটি ব্র্যাঞ্চ মিলিত হয়েছে এবং তীর চিহ্ন দ্বারা ব্র্যাঞ্চ কারেন্ট এর দিক নির্দেশ করা হচ্ছে। দেখা যাচ্ছে I1 ও I2 নোডে প্রবেশ করছে, এবং I3 ও I4 নোড থেকে বেরিয়ে যাচ্ছে। এবার ঐ নোডে যদি কার্শহফ'স কারেন্ট নীতি প্রয়োগ করা হয় তাহলে লিখা যায়: I1 + I2 = I3 + I4. এখানে মাত্র একটি নোডের উদাহরণ দেয়া হয়েছে। তবে একটি সার্কিটে একাধিক নোড থাকতে পারে। কার্শহফ'স কারেন্ট নীতি প্রয়োগ করে নোডাল অ্যানালাইসিস (Nodal Analysis) নামক একটি পদ্ধতির সাহায্যে সার্কিট সমাধান করা যায়।

স্মরণযোগ্য পয়েন্ট: ১) একটি নোডের সাথে যতগুলো ব্র্যাঞ্চ যুক্ত থাকবে তার সবগুলোকেই বিবেচনা করতে হবে, কোন একটিকেও বাদ দেয়া যাবে না; ২) কারেন্ট এর দিক অনুযায়ী (তীর চিহ্ন লক্ষ্যণীয়) ধনাত্মক ও ঋণাত্মক কারেন্ট চিহ্নিত করতে হবে।

কার্শহফ'স ভোল্টেজ নীতি (KVL): এই নীতি অনুযায়ী যে কোন বদ্ধ সার্কিট বা লুপের মধ্যে ভোল্টেজ এর বীজগণিতীয় যোগফল শূন্য। এক্ষেত্রেও বীজগণিতীয় যোগফল বলার কারণ হচ্ছে ভোল্টেজ ধনাত্মক বা ঋণাত্মক হতে পারে। কার্শহফ'স ভোল্টেজ নীতিকে গণিতের সাহায্যে এভাবে প্রকাশ করা যায়,

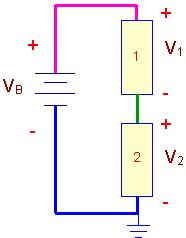
যেখানে m হচ্ছে একটি লুপের মধ্যে মোট ভোল্টেজ এর সংখ্যা। এবার নিচে বাম পাশের এক লুপ বিশিষ্ট সার্কিট ডায়াগ্রামটি লক্ষ্য করুন, যেখানে একটি ভোল্টেজ সোর্স (E) এবং চারটি রোধক আছে। রোধক চারটির বিভব পার্থক্য দেয়া আছে যথাক্রমে E1, E2, E3, ও E4. যে কোন একটি বিন্দু থেকে শুরু করে যদি কার্শহফ'স ভোল্টেজ নীতি প্রয়োগ করা হয় তাহলে লিখা যায়: E - E1 - E2 - E3 - E4 = 0. অনুরূপভাবে, ডান পাশের সার্কিট ডায়াগ্রামে কার্শহফ'স ভোল্টেজ নীতি প্রয়োগ করলে আসে: VB - V1 - V2 = 0. একটি সার্কিটে একাধিক লুপ থাকতে পারে। কার্শহফ'স ভোল্টেজ নীতি প্রয়োগ করে মেশ অ্যানালাইসিস (Mesh Analysis) নামক একটি পদ্ধতির সাহায্যে সার্কিট সমাধান করা যায়।

স্মরণযোগ্য পয়েন্ট: ১) একটি লুপের মধ্যে যতগুলো ভোল্টেজ (Rise/Drop) থাকবে তার সবগুলোকেই বিবেচনা করতে হবে, কোন একটিকেও বাদ দেয়া যাবে না; ২) পোলারিটি অনুযায়ী ধনাত্মক ও ঋণাত্মক ভোল্টেজ চিহ্নিত করতে হবে; ৩) কোন একটি বিন্দু থেকে শুরু করে যে কোন এক দিক দিয়ে (ঘড়ির কাঁটার দিকে কিংবা বিপরীত দিকে) লুপ সম্পন্ন করতে হবে।