আজ যে এলগরিদমটা নিয়ে আলোচনা করব, সেটার নাম মার্জ সর্ট এলগরিদম। শুরুতেই কিছু কথা বলে নেয়া যাক ~ একটা সমস্যা সমাধানের জন্য কয়েকটা এলগরিদম থাকতে পারে। এই যেমন সর্টিং এর জন্য
Bubble Sort, Insertion Sort, Selection Sort, Quicksort, Mergesort, Heapsort এলগরিদম রয়েছে।
প্রশ্ন হচ্ছে এতগুলো এলগরিদমের মধ্যথেকে কোনটা বেছে নিব? এলগরিদমের দুইটা বৈশিষ্টের উপর ভিত্তি করে আমরা বেস্ট এলগরিদম বেছে নিব।
 Correctness
 Efficiency
কিভাবে একটা এলগরিদমের কারেক্টনেস এবং ইফিসিয়েন্সি বের করে সেটা নিয়ে আরেক দিন লেখব। সর্টিং এলগরিদমের মধ্যে সবচেয়ে কার্যকর এলরিদম হচ্ছে Mergesortএলগরিদম। চলুন Mergesort এলগরিদমের সাথে পরিচয় পর্ব শেষ করা যাক। Mergesort এলগরিদমকে Divide and Conquer এলগরিদমও বলাহয়ে থাকে।
১৯৪৫ সালে John von Neumann নামের হাঙ্গেরিয়ান - আমেরিকান গণিতবিদ Mergesort এলগরিদম আবিষ্কার করেন। চলুন শুরু করা যাক 
ধরুন আপনার কাছে আনসর্টেট একটা array আছে, নিচের চিত্রে খেয়াল করুন

আমরা গত পর্বে দেখেছিলাম কিভাবে বাবল সর্ট এলগরিদম ফলো করে খুব সহজেই একটা আনসর্টেড অ্যারে সর্ট করা যায়। এলগরিদম পুরোপুরি ভিন্নভাবে কম সময়ে এই কাজটা সম্পন্ন করে! এজন্য Divide and Conquer নিয়ম ফলো করতে হয়।
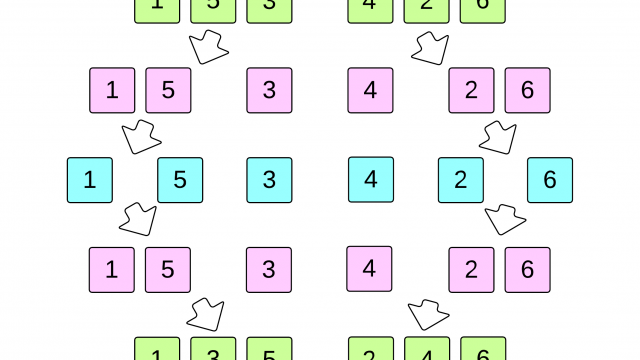
প্রথমেই আনসর্টেড অ্যারেকে দুই ভাগে ভাগ করে নিতে হবে, নিচের চিত্রে খেয়াল করুন

এভাবে যতক্ষণ ভাগ (ডিভাইড) করা যায়, মূলকথা হচ্ছে আমরা মেইন লিস্ট থেকে সাবলিস্ট তৈরি করে বড় সমস্যাটাকে ছোট ছোট অংশে ভাগ করে দিচ্ছি। ছোট অংশগুলোকে যখন সমাধান করে মার্জ করব, তখন আমরা বড় সমস্যাটার সমাধান পেয়ে যাব। চলুন উপরের দুইটা সাবলিস্টকে আবারো ডিভাইড করা যাক

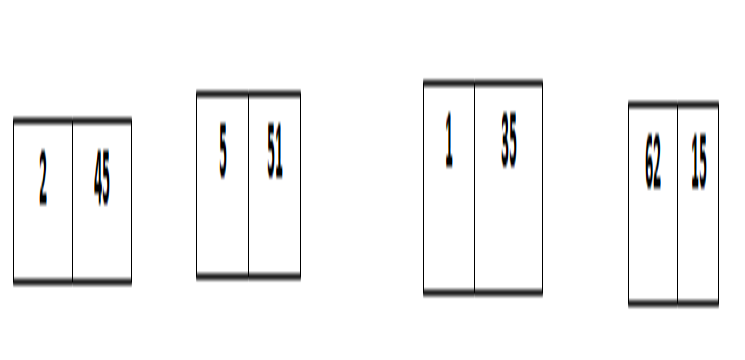
এভাবে আমরা সাবলিস্ট তিরী করতে থাকব যতক্ষণ পর্যন্ত আমাদের সাবলিস্ট বানানোর অপশন থাকবে, নিচের চিত্রে খেয়াল করুন –

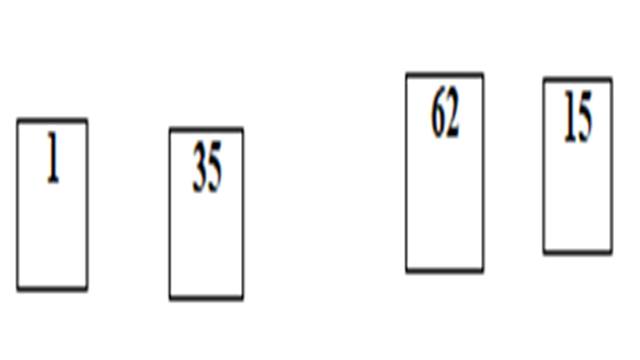
এবারে আর কোন সাবলিস্ট তৈরী করা সম্ভব নয়, এবারে ভাগকরা সর্বশেষ দুইটা এলিমেন্টের মধ্যে কম্পেয়ারিং শুরু করব। যেহেতু ২ < ৪৫, সেহেতু এখানে কোন পরিবর্তন হবে না। ২ আর ৪৫ কে আগের অবস্থায় রেখে দিব। আবার ৫ < ৫১ তাই এখানেও কোন পরিবর্তন হবে না, তাই তাদের কেও আগের অবস্থায় রেখে দিব।
এবারে ডান পাশের ১ এবং ৩৫ এর মধ্যে তুলনা করব, যেহেতু ১<৩৫ সেহেতু ১ এবং ৩৫ আগের অবস্থাতেই থাকবে। এবার ৬২ ও ১৫ এর মধ্যে তুলনা করব, এখানে ৬২ > ১৫, তাই ১৫ আগে চলে আসবে এবং ৬২ পরে চলে যাবে। নিচের চিত্রে খেয়াল করুন!

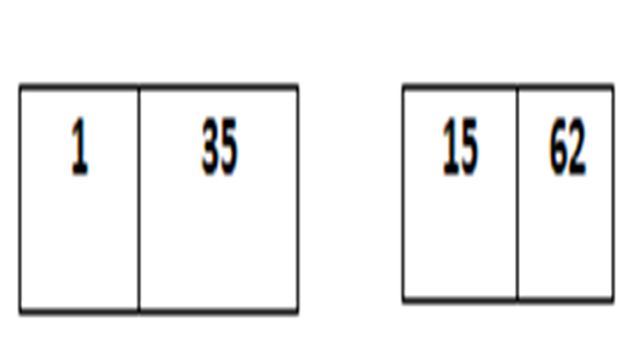
এখন আমাদের হাতে দুইটা দুইটা করে মোট চারটা সেট রয়েছে যেখানে সবাই সর্টেড। এরা মূলত আমাদের ভাগকরা সাবসেট! এবার বাম পাশের দুইটা সেটের প্রথম এলিমেন্টগুলোকে কম্পেয়ার করে সর্ট করব। প্রথমে ২ আর ৫ এর মধ্যে কম্পেয়ার করব, যেহেতু ২< ৫ তাই ২ প্রথম স্থানেই থাকবে! এবারে ৫ এর সাথে ৪৫ কে কম্পেয়ার করব। এখানে ৪৫ > ৫, তাই ৫ চলে আসবে দ্বিতীয় স্থানে। বাকি রইল ৫১, এবার আবার ৪৫ এর সাথে ৫১ কে তুলনা করব। ৪৫ < ৫১ তাই ৪৫ চলে আসবে তৃতীয় স্থানে এবং ৫১ চতুর্থ স্থানে।

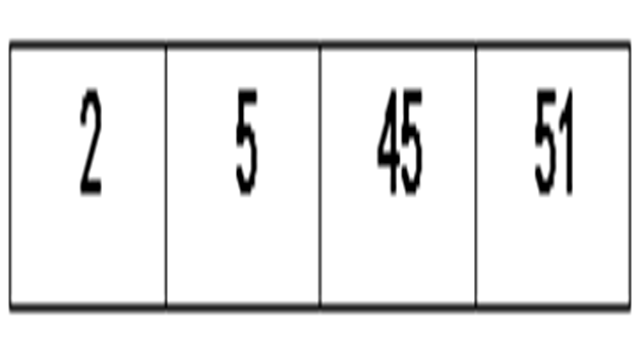
এবার বাম পাশের মতই ডান পাশের দুই সেটের প্রথম এলিমেন্ট একটার সাথে আরেকটার তুলনা করে সর্ট করব। প্রথমে ১ এবং ১৫ এর তুলনা করব। ১ < ১৫ তাই প্রথমে ১ থাকবে, এবার ১৫ এর সাথে ৩৫ এর তুলনা করব। ৩৫ > ১৫, তাই ১৫ চলেযাবে দ্বিতীয় স্থানে। এবার ৩৫ এর সাথে ৬২ দিয়ে তুলনা করব, ৩৫ < ৬২ তাই যথারীতি ৩৫ তৃতীয় এবং ৬২ চতুর্থ স্থানে থাকবে। নিচের চিত্রে লক্ষ করুন ~

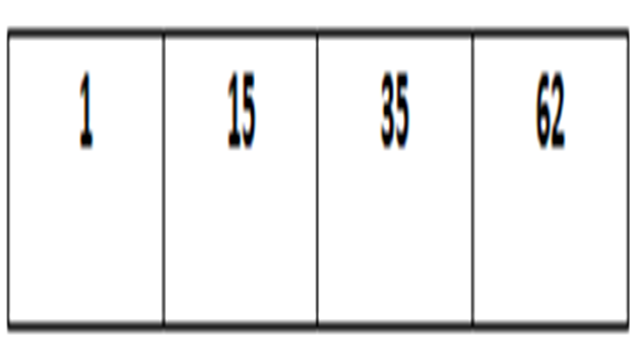
এখন আমাদের হাতে আছে দুইটা সেট, যাদের কে আমরা এতক্ষণ সর্ট করেছি।

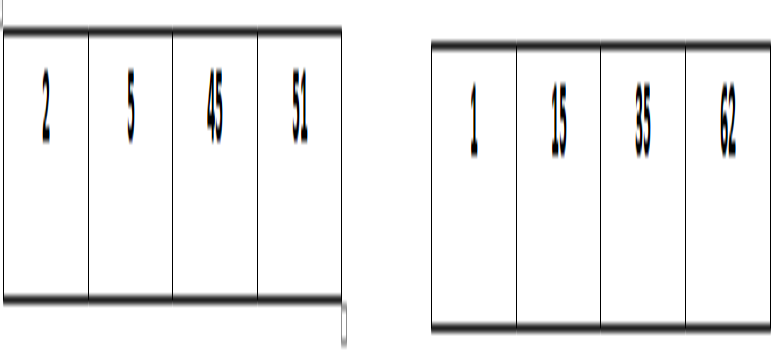
এবার আগের মতই দুই সেটের প্রথম দুইটা এলিমেন্ট একটার সাথে আরেকটার তুলনা করব, প্রথমে ২ এবং ১ এর তুলনা করব। ২> ১ তাই ১ চলে আসবে প্রথমে। এবার ২ এর সাথে ১৫ এর তুলনা করব, এখানে ২ < ১৫ তাই ২ সামনে চলে আসবে। এবার ১৫ এবং ৫ এর তুলনা করব, ১৫>৫ তাই ৫ আগে চলে আসবে। এবার ১৫ এর সাথে ৪৫ এর তুলনা করব, ১৫ <৪৫ তাই ১৫ আগে চলে আসবে।
এবার ৪৫ এর সাথে ৩৫ এর তুলনা করব, ৪৫ > ৩৫ তাই ৩৫ আগে চলে আসবে। এবার ৪৫ এবং ৬২ এর তুলনা করব, ৪৫ < ৬২ তাই ৪৫ আগে চলে আসবে। এবার ৬২ এবং ৫১ এর তুলনা করব, ৬২ > ৫১ তাই ৫১ আগে। এবারে ৬২র সাথে তুলনা করার মত কোন ইলিমেন্ট নেই তাই ৬২ সবার পরে চলে যাবে। নিচের চিত্রে খেয়াল করুন ~

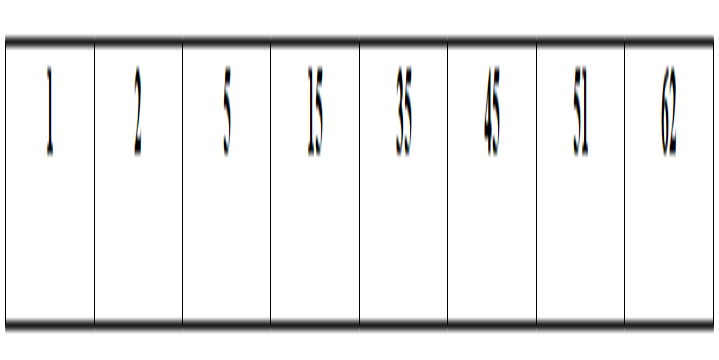
পুরো ব্যাপারটা হচ্ছে, প্রথমে আমরা অ্যারেকে দুই ভাগে ভাগ করতে থাকব, যতক্ষণ পর্যন্ত সিঙ্গেল এলিমেন্ট না হয়। তারপরে সর্ট করে করে নিচ থেকে উপর পর্যন্ত যাব। এটাকে রিকার্সন বলা হয়।

আর এই পর্যন্তই, কোন প্রশ্ন থাকলে টিউমেন্টে অথবা মেইল করতে পারেন!