ভূমিকা

বাস্তব জীবনের প্রতিটি ক্ষেত্রে ছড়িয়ে ছিটিয়ে আছে শিক্ষা। আমরা সবসময় কিছু না কিছু শিখছি। কেউ স্কুল, কলেজ, ভার্সিটিতে পাঠ্যবই থেকে শিক্ষা অর্জন করছি। প্রত্যেকেই আবার সমাজ থেকে কিছু না কিছু সবসময়ই শিখেই চলেছি। কিন্তু কি হবে এতোকিছু শিখে? প্রশ্নটা শুধু আমার বা আপনার না। জগতের সব শিক্ষার্থীর কাছেই এটা সবচেয়ে কমন প্রশ্ন। আমার আগের আর্টিকেলে আমি দেখিয়েছিলাম কম্পিউটার ইঞ্জিনিয়ারিং এর ক্ষেত্রে গণিতের প্রয়োজনীয়তা। গণিত যে কম্পিউটার সাইন্সের বিশাল একটা অংশ জুড়ে রয়েছে তার সামান্য প্রতিফলন ঘটানোর চেষ্টা করেছিলাম আগের আর্টিকেলে। আজকে আরও বিস্তারিত দেখাব।

আগের আর্টিকেল টা এখান থেকে দেখে নিতে পারেনঃ-

ইঞ্জিনিয়ারিং পড়তে এসে কেন আমাকে পদার্থ, রসায়ন পড়তে হবে?

আলোচনার বিষয়

পদার্থ, রসায়নের বিভিন্ন বিষয়ের সাথে কম্পিউটার ইঞ্জিনিয়ারিং এর যোগসূত্র নিয়ে আর্টিকেল লেখা বাকী আছে। কিন্তু ব্যক্তিগতভাবে ব্যস্ততম একটা সময়ের মধ্য দিয়ে যাচ্ছি। সামনে এইচএসসি পরীক্ষা। সারাদিন কলেজ, কোচিং, আর পড়ার মধ্যে ডুবে থাকতে হচ্ছে। এমন সময় আর্টিকেল লেখার জন্য সময় বের করা কত দুঃসাধ্য তা নিশ্চয়ই বুঝতে পারছেন। যাই হোক, এইচএসসি পরীক্ষার জন্য সবাই দোয়া করবেন। গতদিন আমরা সরলরেখার বিভিন্ন অংক এবং প্রোগ্রাম করেছিলাম। ওয়েবপেজ এ কিভাবে সরলরেখা, ত্রিভূজ, চতুর্ভূজ ইত্যাদি রেখাকৃতির সবকিছু আঁকা যায় তার কিছু উদাহরণ দেখিয়েছিলাম। আজকে তার বিপরীত, বা বক্ররেখা নিয়ে কিছু দেখাব। সুতরাং, আজকের আলোচনার বিষয় দাঁড়াচ্ছেঃ-

১। ইঞ্জিনিয়ারিং এ গণিতের প্রয়োজনীয়তা ও বক্ররেখার ব্যবহার

২। ওয়েবপেজ এ বৃত্ত আঁকার কঠিনতম পদ্ধতি (The Hardest Way)

বক্ররেখা নিয়ে কিছু কথাঃ-

দুইটি বিন্দুর সরাসরি সংযোগে হয় একটি সরলরেখা। বক্ররেখা তার বিপরীত। এক্ষেত্রে বিন্দুটি সোজা পথে না গিয়ে বারবার দিক পরিবর্তন করবে। যেসব রেখা বারবার দিক পরিবর্তন করে একটি বিন্দুর সাথে অপর বিন্দুর সংযোগ ঘটায় সেগুলোই বক্ররেখা। নিচের চিত্রটা দেখুনঃ-

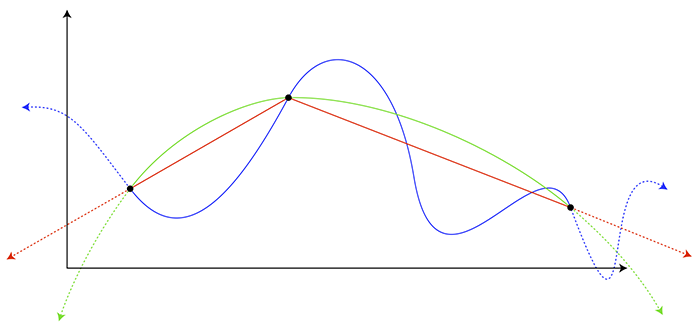
বক্ররেখা বিভিন্ন প্রকারের হয়ে থাকে। সাধারণত, বক্ররেখার কোনো নির্দিষ্ট সমীকরণ হয় না। কারণ, বক্ররেখা কোনো নির্দিষ্ট নিয়ম মেনে চলেনা। তাই বক্ররেখা আঁকার জন্য তার মধ্যস্থিত ক্ষুদ্রতম (dx) ব্যাবধান পর পর বিভিন্ন বিন্দুর স্থানাংক নিয়ে সেগুলো যোগ করা হয়। তবে কিছু বিশেষ প্রকারের বক্ররেখাকে নির্দিষ্ট সমীকরনের মাধ্যমে প্রকাশ করা যায়। যেসব বক্ররেখা নির্দিষ্ট নিয়ম মেনে চলে তাদের সমীকরণ নির্ণয় করা যায়। এরুপ কিছু বক্ররেখা হলঃ-

১) বৃত্ত

২) অনুপ্রস্থ তরঙ্গ এবং অগ্রগামী তরঙ্গ

৩) বিভিন্ন ত্রিকোণোমিতিক লেখচিত্রঃ সাইনের লেখ, কোসাইনের লেখ ইত্যাদি।

যেহেতু এগুলো নির্দিষ্ট নিয়ম মেনে চলে। তাই এদেরকে সমীকরণের মাধ্যমে প্রকাশ করা যায়। সময়স্বল্পতার কারণে আজকে শুধু বৃত্ত নিয়ে এক্সপেরিমেন্ট করব। তরঙ্গ এবং ত্রিকোণমিতিক লেখচিত্র পরে কখনও দেখা যাবে।

বৃত্ত

আগের আর্টিকেলে যেমন সরলরেখার সংজ্ঞা থেকে সরলরেখা এঁকেছিলাম। আজকে বৃত্তের সংজ্ঞা থেকে বৃত্ত আঁকব।

বৃত্তঃ কোনো নির্দিষ্ট বিন্দু থেকে সমদূরবর্তী সকল বিন্দুর সঞ্চারপথকে বৃত্ত বলে।

সুতরাং, বৃত্তের একটা নির্দিষ্ট বিন্দু থাকতে হবে। তাকে কেন্দ্র বলা হয়। আর বৃত্তের পরিধির মধ্যে সকল বিন্দু থেকে কেন্দ্রের দূরত্ব নির্দিষ্ট থাকতে হবে। যাকে ব্যাসার্ধ বলা হয়।

সুতরাং, কেন্দ্র এবং ব্যাসার্ধ থাকলেই একটি বৃত্ত এঁকে ফেলা যায়। বীজগাণিতিক স্থানাংক ব্যবস্থায় কেন্দ্রকে (h, k) এবং ব্যাসার্ধকে r ধরা হয়।

এবার একটু স্কুল লাইফে ফিরে যান। স্যার বৃত্ত আঁকতে বললে কিভাবে আঁকতেন? প্রথমে কম্পাসের কাঁটা খাতায় বসিয়ে কম্পাস একটু ফাঁক করে তার চারদিক দিয়ে পেন্সিল টেনে আনতেন। আমরা প্রায় সমপর্যায়ের একটি পদ্ধতি ব্যবহার করব আজকের এক্সপেরিমেন্টে।

প্রথমে ওয়েবপেজ এ একটা ভার্চুয়াল গ্রাফ পেপার তৈরী করে নিই। ভার্চুয়াল গ্রাফ পেপার তৈরীর পদ্ধতি আগের আর্টিকেলে দেখানো হয়েছে। তাহলে আমাদের কাছে নিচের মত একটি গ্রাফ আছেঃ-

এখানে আমরা বৃত্ত আঁকব। যদিও হাইস্কুলের পদ্ধতিই ব্যবহার করব। তবে বাজে ব্যাপারটা হল, প্রোগ্রামিং এ কম্পাসের মত কোনো জিনিস নেই। তাই আমরা কেন্দ্র থেকে ব্যাসার্ধের সমান দূরত্বে সব বিন্দুর স্থানাংক নির্ণয় করব। খাতা কলমে বসলে সম্ভবত ছোট একটা বৃত্তের জন্যও এই কাজটা করতে কয়েকদিন সময় লাগতো। কিন্তু কম্পিউটার এই কাজটা এক সেকেন্ডেরও কম সময়ে করে ফেলতে পারবে।

বৃত্ত আঁকার পদ্ধতি

ওয়েবপেজ এ বৃত্ত আঁকার জন্য খুব সহজ একটা পদ্ধতি আছে। একটা বর্গ (ডিভ দিয়ে) এঁকে নিয়ে তার বাহুর অর্ধেকের সমান ব্যাসার্ধ নিয়ে border-radius সিএসএস প্রোপার্টি দিয়ে দিলেই হয়। কিন্তু আসলেই কি কম্পিউটারে বৃত্ত আঁকা এতো সহজ? যারা ওয়েবপেজ এর বাইরেও সি বা জাভা নিয়ে কাজ করেছেন তাঁরা জানেন বৃত্ত আঁকার জন্য কম্পিউটার ভেতরে কত জটিল প্রকৃয়া সম্পন্ন করে। আজকে আমরা জাভাস্ক্রিপ্টে তা দেখব। তাহলে, চলুন দেখা যাক How It Works?

বৃত্তের জন্য আমাদের শুধু কেন্দ্র আর ব্যাসার্ধ জানা থাকলেই হবে। ধরে নিই, বৃত্তের কেন্দ্রের স্থানাংক (h, k) এবং ব্যাসার্ধ r। এর সঞ্চারপথের বিভিন্ন বিন্দুর স্থানাংক নির্ণয়ের জন্য আমাদের বৃত্তের সমীকরণ ব্যবহার করতে হবে। বৃত্তের সমীকরণ হলঃ-

(x-h)²+(y-k)²=r²

=> x²-2hx+h²+y²-2ky+k²-r²=0

=> x²+y²-2hx-2ky+h²+k²-r²=0

প্রথমে, গ্রাফের নিয়মেই x এর বিভিন্ন মান ধরব। কিন্তু এই মানের লিমিট কি? কত থেকে কত’র মধ্যে ধরতে হবে? বৃত্তের কেন্দ্র থেকে ধরলে x এর সর্বোচ্চ মান হবে তার কেন্দ্র আর ব্যাসার্ধের যোগফলের সমান। আর সর্বনিম্ন মান হবে কেন্দ্র আর ব্যাসার্ধের বিয়োগফলের সমান। সুতরাং,

xmin=(r-h) এবং xmax=(r+h)

এই সীমার মধ্যে x এর বিভিন্ন মানের জন্য y এর স্থানাংক নির্ণয় করব। এজন্য ব্যবহার করব “ফর লুপ” পদ্ধতি। অনুরূপভাবে ওয়াই এর জন্য এক্স এর বিভিন্ন স্থানাংক নির্ণয় করব।

সুতরাং, x এর মান দেয়া থাকলে y এর মান হবেঃ-

x²+y²-2hx-2ky+h²+k²-r²=0

=> y²-2ky+x²-2hx+h²+k²-r²=0

=> y²-2ky+c=0

­­­এটি একটি ওয়াই এর দ্বিঘাত সমীকরণ (ax²+bx+c=0 আকৃতির)। যেখানে, a=1, b=-2k, c=c। সুতরাং, দ্বিঘাত সমীকরণের সমাধানের কোয়াড্রাটিক ফরমূলা থেকে (সরাসরি c এর মান বসিয়ে) পাইঃ-

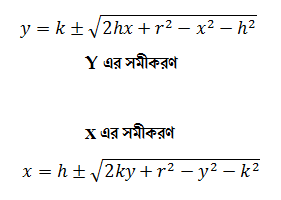
অনুরূপভাবে ওয়াই এর বিভিন্ন মানের জন্য এক্স এর বিভিন্ন মান পাওয়ার জন্য কোয়াড্রাটিক ফরমূলা থেকে উপরের সমীকরণ পাই। কোয়াড্রাটিক ফরমূলা সম্পর্কে প্রায় সবাই জানেন। তারপরও বিস্তারিত জানতে এখানে দেখতে পারেন।

এই দুটি সূত্র থেকেই আমরা ফাংশন তৈরী করে বৃত্ত আঁকতে পারব। এখানে এক্স এর একটি মানের জন্যই ওয়াই এর দুইটি মান পাওয়া যায়। অনুরুপভাবে ওয়াই এর জন্যও এক্স এর দুইটি মান পাওয়া যায়। তাই চারবার লুপ করতে হবে আমাদের।

প্রথমে জাভাস্ক্রিপ্টে একটা ফাংশন বানাই যা আর্গুমেন্ট হিসেবে একটি অ্যারে এবং একটি ইন্টেজার নেবে।
function circle(C, r){}
এখানে সি একটি অ্যারে এবং আর একটি সংখ্যা। সি এর মাধ্যমে বৃত্তের কেন্দ্র এবং আর দিয়ে ব্যাসার্ধ বোঝানো হয়েছে।

কেন্দ্রের স্থানাংক দেখিয়ে ফাংশনটি হবেঃ-
function circle(C, r){var h=C[0], k=C[1];}
এখন, x এর মান r-h থেকে r+h সীমার মধ্যে নিয়ে ফর লুপ করলে y এর অনেকগুলো মান পাওয়া যাবে। সমীকরণটি থেকে দুই রকম মান পাওয়া যাবে। রুট কে ধনাত্বক ধরে একবার এবং রুট কে ঋণাত্বক ধরে একবার। সুতরাং লুপ হবে নিচের মতঃ-
for (i=(h-r);i<=(h+r);i+){x=i;
y=k+Math.sqrt(2*h*x)+(r*r)-(x*x)-(h*h));}
রুট করার জন্য এখানে জাভাস্ক্রিপ্টের Math.sqrt ফাংশন ব্যবহার করা হয়েছে। ওয়াই এর জন্য রুট কে একবার ধনাত্বক ও একবার ঋণাত্বক। ওয়াই এর জন্যও অনুরূপ। ফলে মোট চারবার লুপ করতে হয়েছে আমাদের। ফলে সবশেষে আমরা নিচের মত একটা ফাংশন পাব, যা দ্বারা যে কোনো বৃত্ত অংকন করা যাবেঃ-
function circle(C, r){var h=C[0], k=C[1];
for (i=(h-r);i<=(h+r);i+){x=i;
y=k+Math.sqrt(2*h*x)+(r*r)-(x*x)-(h*h));
document.write("<div class='point' style='left:"+x+"px;bottom:"+y+"px;'></div>");}
for (i=(h-r);i<=(h+r);i+){x=i;
y=k-Math.sqrt(2*h*x)+(r*r)-(x*x)-(h*h));
document.write("<div class='point' style='left:"+x+"px;bottom:"+y+"px;'></div>");}
for (i=(k-r);i<=(k+r);i+){y=i;
x=h+Math.sqrt(2*k*y)+(r*r)-(y*y)-(k*k));
document.write("<div class='point' style='left:"+x+"px;bottom:"+y+"px;'></div>");}
for (i=(k-r);i<=(k+r);i+){y=i;
x=h-Math.sqrt(2*k*y)+(r*r)-(y*y)-(k*k));
document.write("<div class='point' style='left:"+x+"px;bottom:"+y+"px;'></div>");}

ব্যাস। হয়ে গেল আমাদের বৃত্তের ফাংশন। এখন এই ফাংশন এ প্রথম আর্গুমেন্টে বৃত্তের কেন্দ্রের স্থানাংক এবং দ্বিতিয় আর্গুমেন্টে ব্যাসার্ধ দিলেই বৃত্ত এঁকে যাবে। তাহলে চলুন একটা লাইভ ডেমো দেখা যাক।

# উপরের ফাংশন দিয়ে বৃত্ত আঁকার ডেমো

সাইন্স বা প্রোগ্রামার নন যারা, তাদের জন্যঃ-

অনেকেই সাইন্স ব্যাকগ্রাউন্ডের না হওয়ায় আগের আর্টিকেলের ব্যাপারে অনেক প্রশ্ন করেছেন। তাদের জন্য এবং যারা প্রোগ্রামিং করেন না তাদের জন্য কিছু ডেমো ওপেন ওয়েব এপ্লিকেশন বানিয়েছি। আপনারা ইচ্ছে করলে ভিজুয়ালি সরলরেখা এবং বৃত্ত আঁকতে পারবেন অনলাইনে।
১। সরলরেখা আঁকার প্রোগ্রাম (যে কোনো দুইটি বিন্দুর স্থানাংক দিলেই সরলরেখা এঁকে যাবে)
২। বৃত্ত আঁকার প্রোগ্রাম (কেন্দ্র ও ব্যাসার্ধ দিলেই এঁকে যাবে)
[সতর্কতাঃ বৃত্তের প্রোগ্রামে জাভাস্ক্রিপ্ট ইঞ্জিনের বেশ কিছু বেসিক প্রোগ্রাম ব্যবহার করতে হয়েছে। তাই কেন্দ্র মূলবিন্দু (০, ০) তে ধরার চেষ্টা করবেন। নতুবা র‍্যাম কম হলে ব্রাউজার হ্যাং করতে পারে। ভেতরে জটিল কিছু হিসেব করতে হয়, তাই এমনটা হয়েছে। তাছাড়া জাভাস্ক্রিপ্টে এইচটিএমএল ডম এপেন্ড করতে বাধ্য হয়েছি (এছাড়া অন্য উপায়ও নেই), তাই খানিকটা স্লো। তাই মূলবিন্দুকেই কেন্দ্র ধরলে ভালো ফলাফল পাবেন।

উপসংহারঃ-

পাঠ্যবইয়ের বিষয়বস্তু যত ঝামেলার মনে হয় এগুলো ততই উপকারী। বিজ্ঞান নিয়ে যারা কাজ করতে চান তাদের জন্য এগুলো অতীব গুরুত্বপূর্ণ। তাই এবিষয়ে সর্বোচ্চ জ্ঞান অর্জন করার চেষ্টা করতে হবে আমাদের। দেশকে এগিয়ে নিয়ে যেতে তো আমাদেরই কাজ করতে হবে। তাছাড়া, জীবনটা কি শুধুই উপভোগ করার জন্য?
যাই হোক, সময়স্বল্পতার জন্য আজকে শুধু বৃত্ত দেখিয়েই ক্ষান্ত দিতে হল। আগামীবার ইনশাল্লাহ সময় করে অগ্রগামী তরঙ্গ বা অনুপ্রস্থ তরঙ্গ এবং সাইন কোসাইন প্রভৃতির লেখচিত্র আঁকার ফাংশন তৈরী করব। আপনারাও ইচ্ছে করলে এগুলো প্র্যাকটিস করতে পারেন। আর আমার আসন্ন এইচএসসি পরীক্ষার জন্য দোয়া করবেন সবাই। কারও কোথাও প্রশ্ন থাকলে আমার সঙ্গে ফেসবুকে যোগাযোগ করতে পারেন। ফেসবুকঃ http://www.facebook.com/arif.reza.rifat
Find Me On Facebook

সবাইকে ধন্যবাদ জানিয়ে আজকের আর্টিকেল শেষ করছি। সবাই ভালো থাকুন, সুস্থ থাকুন। আর বেশী বেশী করে জ্ঞান অর্জন করতে থাকুন।